红黑树

# 红黑树

# 介绍

红黑树，Red-Black Tree 「RBT」是一个自平衡二叉查找树(BST)，树上的每个节点都遵循下面的规则:

1. 每个节点都有红色或黑色
2. 树的根始终是黑色的
3. 没有两个相邻的红色节点（红色节点不能有红色父节点或红色子节点，并没有说不能出现连续的黑色节点）
4. 从节点（包括根）到其任何后代NULL节点(叶子结点下方挂的两个空节点，并且认为他们是黑色的)的每条路径都具有相同数量的黑色节点

# 插入

# 重标记颜色

假设插入的新节点为 X

1. 将新插入的节点标记为红色
2. 如果 X 是根结点(root)，则标记为黑色
3. 如果 X 的 parent 不是黑色 且 X 的 uncle (叔叔) 是红色

• 3.1 将 parent 和 uncle 标记为黑色
• 3.2 将 grand parent (祖父) 标记为红色
• 3.3 让 X 节点的颜色与 X 祖父的颜色相同，然后重复步骤 2、3

（X 的 parent 不可能同时是红色又是 root (步骤二确定root一定是黑色)）

# 举例

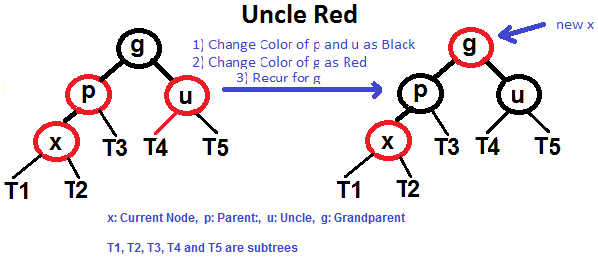
• 将新插入的 X 节点标记为红色
• 发现 X 的 parent (P) 同样为红色，这违反了红黑树的第三条规则「不能有两个连续相邻的红色节点」
• 发现 X 的 uncle (U) 同样为红色
• 将 P 和 U 标记为黑色
• 将 X 和 X 的 grand parent (G) 标记为相同的颜色，即红色，将 G 做为新的 X，继续重复公式 2、3
• 发现 G 是根结点，标记为黑色

# 旋转

如果 X 的 parent 不是黑色 且 X 的 uncle (叔叔) 是黑色

• 左左

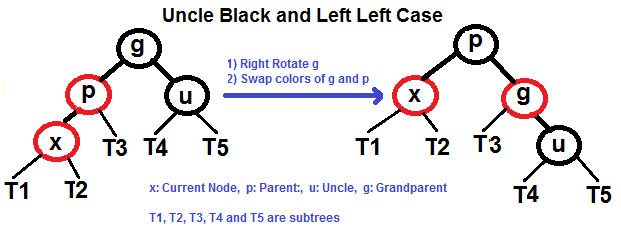
将 X 的 parent P 和 祖父 G 交换, 将 G 作为 P 的右节点， P 原本的右节点作为祖父的左节点, 即 P.right, G.left = G, P.right;

• 左右

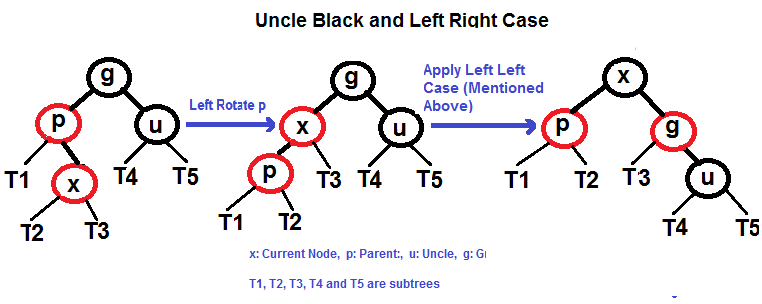
先将 P 和 X 交换， P 作为 X 的左节点, X 原本的左节点作为P的右节点, 即 X.left, P.right = P, X.left

然后使用左左的规则

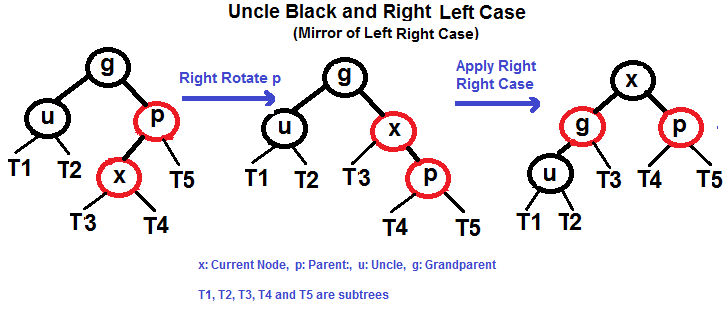
• 右右类似左左

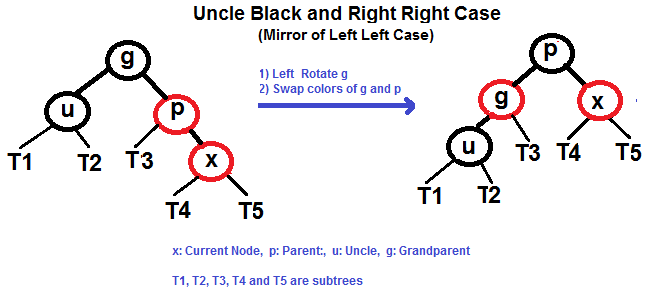
• 右左类似左右

# 删除